7.4. Estimation of stable age distribution

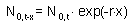
Substituting this equation into [3] we get the relationship between the number of organisms in age x and in age 0 in a stable age distribution:

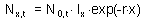
Now we can estimate the proportion of organisms, c , in age x:

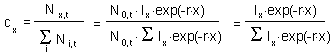[7]

Age, x	lx	exp(-rx)	lxexp(-rx)	cx	Simulated cx
0	1.000	1.0000	1.0000	0.2413	0.2413
1	0.845	0.8507	0.7188	0.1734	0.1734
2	0.824	0.7237	0.5963	0.1439	0.1439
3	0.795	0.6156	0.4894	0.1181	0.1181
4	0.755	0.5237	0.3954	0.0954	0.0954
5	0.699	0.4455	0.3114	0.0751	0.0751
6	0.626	0.3790	0.2373	0.0572	0.0572
7	0.532	0.3224	0.1715	0.0414	0.0414
8	0.418	0.2743	0.1147	0.0277	0.0277
9	0.289	0.2333	0.0674	0.0163	0.0163
10	0.162	0.1985	0.0322	0.0078	0.0078
11	0.060	0.1689	0.0101	0.0024	0.0024
Total			4.1445	1.0000	1.0000

Age distribution estimated using equation [7] (column 5) coincided with simulated age distribution after 50 iterations of the model.